Zákon zachovania hybnosti - videodemonštrácie
Fyzikálne video-experimenty
Hlavná ponuka:
Zákon zachovania hybnosti
Motivácia
Prečo sa fén, ktorý je pripevnený na vozíček s kolieskami, po jeho zapnutí začne pohybovať?
Experiment
Video experimentu 
Použité pomôcky
- fén
- vozíček
- lepiaca páska
Vysvetlenie
Zákon zachovania hybnosti hovorí, že v izolovanej sústave sa hybnosť sústavy zachováva, t.j.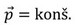 
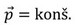
Pod hybnosťou sústavy rozumieme vektorový súčet hybnosti jednotlivých telies, ktoré sústavu tvoria
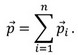
Napríklad sústavu tvorí vozík s pieskom a strela, ktorá letí oproti nemu. Zo zákona zachovania hybnosti vyplýva, že hybnosť sústavy v dvoch rôznych situáciách musí byť rovnaká (napr. pred zrážkou strely s vozíkom a po ich zrážke). Potom hybnosť tejto sústavy pred zrážkou bude daná súčtom hybnosti vozíka a strely. Po zrážke, ak strela uviazne v piesku, bude mať sústava spoločnú hmotnosť (danú súčtom hmotnosti vozíka s pieskom a strely) a spoločnú rýchlosť. Potom hybnosť sústavy je daná súčinom spoločnej hmotnosti a spoločnej rýchlosti sústavy.
V experimente na videu izolovanú sústavu tvorí fén a vzduch za fénom. Pred zapnutím fénu je hybnosť sústavy rovná nule (fén a vzduch sú v pokoji) 
. Po zapnutí fénu, sa začne vzduch za fénom pohybovať, jeho hybnosť je 
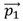. Hybnosť fénu označme 
. Potom hybnosť sústavy po zapnutí fénu je 
. Zo zákona zachovania hybnosti vyplýva, že hybnosť sústavy pred zapnutím fénu sa musí rovnať hybnosti sústavy po zapnutí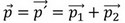 
. Pre veľkosť hybnosti platí 
, kde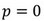 
. Odtiaľ pre hybnosť fénu 
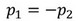. V dôsledku zachovania hybnosti sústavy (jej hybnosť musí byť rovná nule aj po zapnutí fénu) sa fén začal pohybovať opačným smerom ako vzduch za fénom.
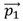. Po zapnutí fénu, sa začne vzduch za fénom pohybovať, jeho hybnosť je . Hybnosť fénu označme . Potom hybnosť sústavy po zapnutí fénu je . Zo zákona zachovania hybnosti vyplýva, že hybnosť sústavy pred zapnutím fénu sa musí rovnať hybnosti sústavy po zapnutí 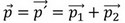. Pre veľkosť hybnosti platí , kde 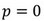. Odtiaľ pre hybnosť fénu 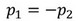. V dôsledku zachovania hybnosti sústavy (jej hybnosť musí byť rovná nule aj po zapnutí fénu) sa fén začal pohybovať opačným smerom ako vzduch za fénom.Otázky
- Vysvetlite pomocou zákona zachovania hybnosti, prečo sa dá loďka nachádzajúca sa v pokoji na vodnej hladine do pohybu, keď sa po nej prejdete od jedného jej konca na druhý?
- Strela s hmotnosťou 20 g vyletí z hlavne pušky rýchlosťou 760 m/s. Akú hmotnosť má puška, ak spätným nárazom získala v opačnom smere rýchlosť 2,7 m/s .
- Bežiaca mačka hmotnosti 3 kg s rýchlosťou 5 m/s vyskočí na skejtbord, ktorý je v pokoji. Aká je hybnosť skejtbordu, mačky a sústavy mačka + skejtbord pred skokom mačky? Aká je hybnosť sústavy mačka a skejtbord, keď sa mačka na ňom vezie? Akou rýchlosťou sa vezie mačka na skejtborde?
- Krasokorčuliar s hmotnosťou 75 kg ide po ľade rýchlosťou 1,2 m/s a uchopí stojacu krasokorčuliarku s hmotnosťou 45 kg, ďalej už idú spoločne. Aká je hybnosť krasokorčuliara a krasokorčuliarky pred uchopením krasokorčuliarom? Ako bude daná ich spoločná hybnosť po uchopení? Akou spoločnou rýchlosťou sa budú pohybovať?
- Železničný vagón o hmotnosti 10 ton sa pohybuje rýchlosťou 54 km/h. Druhý vagón, ktorý má hmotnosť 30 ton sa pohybuje s rýchlosťou 4 m/s. Oba vagóny sa zrazia a zostanú zakliesnené. Akou veľkou rýchlosťou sa spojené vagóny pohybujú, ak sa pred zrážkou pohybovali a) rovnakým, b) opačným smerom?
Ak nevieš odpovedať na otázky, pozri si ešte raz video a vysvetlenie.
Použité zdroje:
http://fyzika.jreichl.com/main.article/view/33-zakon-zachovani-hybnosti
http://www.oskole.sk/?id_cat=3&clanok=1433