Stavová rovnica - videodemonštrácie
Fyzikálne video-experimenty
Hlavná ponuka:
Stavová rovnica
Motivácia
Zdeformovanú stolnotenisovú loptičku je možné narovnať tak, že ju dáme do teplej vody. Je možné zmeniť objem nafuknutého balónika bez toho, že by sme ho museli nahriať v teplej vode? Pozri nasledujúce video.
Experiment
Video experimentu 
Použité pomôcky
- vákuový zvon
- 2 balóny
Vysvetlenie
Stav plynu v uzavretom priestore možno charakterizovať stavovými veličinami – tlakom p, objemom V, teplotou T a počtom molov n, pre ktoré platí tzv. stavová rovnica
kde R = 8,314 J/K.mol je univerzálna plynová konštanta. Počet častíc plynu možno určiť zo vzťahu
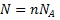
kde 
je Avogadrovo číslo. Stavová rovnica umožňuje popísať zmenu dvoch stavov plynu, ak sa mení niektorá alebo aj viaceré zo stavových veličín.
je Avogadrovo číslo. Stavová rovnica umožňuje popísať zmenu dvoch stavov plynu, ak sa mení niektorá alebo aj viaceré zo stavových veličín.Vzduch v nafúknutom balóne vo video-experimente má objem V 1 a jeho tlak p 1 je väčší ako atmosférický tlak p 1´ lebo musí kompenzovať aj tlak pružných síl stien balóna, ktoré vzduch stláčajú. Pri malých zmenách objemu balóna možno predpokladať, že tlak elastických síl je konštantný. Stena balóna je teda v pokoji, ak platí
.Stavová rovnica pre vzduch v balóne bude mať tvar
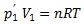.V dôsledku zníženia tlaku vo zvone z hodnoty p 1 na hodnotu p 2, sa vzduch balóne rozpína, kým jeho tlak neklesne na hodnotu
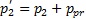
a stavová rovnica potom bude mať tvar
. Ak predpokladáme, že plyn v balóne mal v oboch stavoch rovnakú teplotu, platí
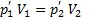. Zväčšenie objemu balóna na hodnotu pri znížení tlaku vo zvone možno vyjadriť vzťahom
.Ak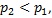 
potom 
ako možno vidieť aj na video-experimente. Zmenou tlaku vzduchu v balóniku, dosiahneme zmenu jeho objemu. V prípade zdeformovanej stolnotenisovej loptičky zmenu jej objemu dosiahneme ponorením do teplej vody, čím sa zvýši tlak vzduchu v loptičke. Následne tlaková sila narovná zdefermované steny loptičky. Došlo k zmene tlaku, objemu a teploty vzduchu v loptičke.
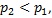potom ako možno vidieť aj na video-experimente. Zmenou tlaku vzduchu v balóniku, dosiahneme zmenu jeho objemu. V prípade zdeformovanej stolnotenisovej loptičky zmenu jej objemu dosiahneme ponorením do teplej vody, čím sa zvýši tlak vzduchu v loptičke. Následne tlaková sila narovná zdefermované steny loptičky. Došlo k zmene tlaku, objemu a teploty vzduchu v loptičke. Otázky
- Počas experimentu s balónom vo vákuovom zvone objem uzavretého balóna, v ktorom je vzduch, vzrástol o 10%. Koľkokrát sa zmenšil tlak vzduchu v balóne?
- Koľko častíc vzduchu je v miestnosti s rozmermi 2,5 x 4 x 2,5 m3 za normálneho atmosférického tlaku 101,325 kPa. V miestnosti je 20°C.
- V dvoch rovnakých oceľových fľašiach je kyslík. Ako možno zistiť tlakomerom, v ktorej fľaši je viac kyslíka? Vysvetlite pomocou stavovej rovnice.
- Pomocou stavovej rovnice vysvetlite princíp letu teplovzdušného balóna.
Ak nevieš odpovedať na otázky, pozri si ešte raz video a vysvetlenie.
Použité zdroje:
Blaško M., Gajdušek, J., Kireš, M., Onderová, Ľ. 2004: Fyzika mmolekulová fyzika a termodynamika. 1.vydanie. Bratislava. SPN - Mladé letá, s.r.o. 2004. ISBN 80-10-00008-6.